Ejercicio del Método de Vogel

1* Requiere de una penalizacion para cada renglon. Restando el menor elemento de costo del renglón.

Supongamos que a una empresa transnacional que tiene 3 plantas R,S,T estas surten un producto hacia alamacenes A,B,C,D,E,F,G que forman parte del grupo empresarial debemos considerar lo relacionado al costo de transporte desde la planta a cada alamacen.

Metodo de Vogel (VAM)

Este método es heurístico y suele producir una mejor solución inicial. De echo VAM suele producir una solución inicial óptima, o próxima a nivel óptimo. Es un método que trabaja sobre el ahorro.

Ejercicio de Asignaciòn

Necesitamos procesar 4 tareas para la cual contamos con 4 maquinas.

El desperdicio que producimos de las tareas por maquina dada una matriz, expresemos esto en pesos y necesitamos definir la asignación óptima.

Como se trata de desperdicios, es un problema de minimizacion.

Primero vemos que todas las casillas tengan un costo

M= renglones

N= columnas

Es igual a 4

*Elegimos el menor valor del renglon y lo restamos a los demas en este caso es 49, 45, 46, 38

Ahora los nuevos valores son:

Los valores mas pequeños son 0,0,5,21

Ahora los nuevos valores son:

En esta tabla solo tenemos 3 lineas parciales por lo que todavia no hayamos lo optimo por lo que tenemos que hacer otra tabla.

Los valores mas pequeños de las 3 filas es 12 lo restamos a los demas respetando los valores que estan en la interseccion.

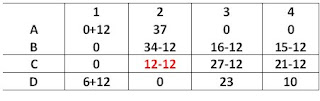
Podemos observar que las lineas indican que 3=4 no es optimo seguimos buscando asignar recursos a las actividades

Ahora el menor nuemro es 3 y se lo restamos a los demas respetando los asignados o intersectados.

Interpretacion:

Realizar la tarea A en la maquina 3 con un costo de 54

Realizar la tarea B en la maquina 3 con un costo de 81

Realizar la tarea C en la maquina 3 con un costo de 46

Realizar la tarea D en la maquina 3 con un costo de 38

El costo total minimo sera de 219 por la asignacion de las tareas en la maquina de la forma mas optima.

Asignaciòn

Este tipo de problemas conocido como problema de asignación, tiene una gran variedad de aplicaciones dentro de la gama de la toma de decisiones. Problemas que constantemente se le presentan a los gerentes de personal, en cuanto a la colocación óptima de personal; a los gerentes de producción en cuanto a la utilizacion óptima de equipo con diferentes porcentajes de eficiencia en relación a diferentes tareas y trabajos, etc.

El problema de asignación es un caso especial del método de transporte, con las siguientes características:

m= n

ai = 1 para todas las (i)

bj = 1 para todas ls (j)

Lo anterior significa que el número de orígenes o el numero de recursos debe ser igual al numero de destinos o de asignaciones, y que cada origen o recurso con relación al destino o asignación debe corresponder a uno. Igualmente se requiere que:

Xij = 0 o Xij = 1

Es decir, que cada origen o recurso tiene que estar "asignado" o seleccionado exclusivamente a un destino o auna utilizacion única. Por lo tanto, el problema consiste en determinar como se debe hacer la asignación de recursos para minimizar ya sea el costo, el tiempo, las perdidas, la falta de eficiencia etc.

La técnica mas recomendable para solucionar este tipo de problemas es a través del Método Húngaro el cual consiste en:

1. Balancear el modelo (filas, columnas)

2.Para todo renglón escogemos el menor valor y restarlos a todos los demás en el mismo renglón

3.Para cada columna escogemos el menor valor y restarlos de todos los demás en la misma columna

4. Tachar el mínimo numero de lineas verticales y horizontales de forma que todos los ceros quedan tachados

5. Usar el criterio de optimizacion

6.Seleccionar el menor valor no tachado de toda la matriz. El valor restarlo de todo elemento no tachado y sumarlo a los elementos en al interacción de dos lineas.

7. Hacer los pasos en forma sucesiva buscando tachar todos los ceros, regresar al paso 4 hasta que cada renglón y cada columna tengan una sola asignación.

Para caso de maximizacion:

Seleccionamos el mayor elemento de toda la matriz, este valor restarlo de todos los elementos, los valores negativos representan los costos de oportunidad, lo que indica que se deja de ganar o producir.

Ejercicio del Mètodo Dual

Considerando el siguiente problema primal, calcular su mòdelo dual.

Sea Max: z= 3x+5y

Sujeta a:
x≤ 4
y ≤ 6
3x + 2y ≤ 18
x + 4y ≤ 10

Entonces:
z Min = 4z1 + 6z2 + 18z3 +10z4

Ponemos los coeficentes disponibilidad en forma de vector columna (matriz) Primal.

b=
4
6
18
10

bT= 4 6 18 10

Restricciones:
A=
1 0
0 1
3 2
1 4

AT=
1 0 3 1
0 1 2 4

Funcion Objetivo
C= 3 5

CT=
3
5

El resultado, como consecuencia de un sistema primal a un sistema dual queda de la sigueinte manera:

AT=
1 0 3 1
0 1 2 4

BT= 4 6 18 10

CT=
3
5

Método Dual

Para cualquier problema de Programación Lineal (Primal) debe tener su metodologia Dual.
El problema primal puede tener más restricciones que variables esto significa la solución "Dual". Y debe resolverse por nuevas restricciones.

1. Si el primal se refiere a maximizar el problema Dual sera minimizar
2. Los coeficientes de la funcion objetivo del primal seran los coeficientes del vector de disponibilidad de recursos en el Dual.
3. Asi los coeficientes del vector disponibilidad de recursos del problema primal seran los coeficientes de la funcion objetivo (vector costos, precios o utilidad) en el problema Dual
4. Los coeficientes de las restricciones en el primal (transpuesta de la matriz), sera la matriz de los coeficientes en el Dual.
5.Los signos de desigualdad del problema dual son contrarios a los del problema primal.
6.Las variables "x" del primal se convierten en nuevas variables "y" en el Dual.

Ejercicio de Esquina Noroeste

4 agencias ordenan autos nuevos que deben llegar desde 3 plazas, la agencia A necesita 6 autos, la agencia B requiere de 5, la agencia C 4 y la D requiere 4.

La planta 1 tiene 7 autos en stock, l aplanta 2 tiene 13 y la planta 3 tiene 3. El costo de enviar un auto de la planta a la agencia se puede ver en la tabla.

M+n-1 = 3+5-1= 7 casillas asignadas

Ejercicio del Método de Transporte

Supongamos que una empresa transnacional tiene 3 plantas X,W,Y y estas surten de un producto a 7 almacenes A,B,C,D,E,F,G que forman parte del grupo empresarial. Debemos considerar lo relacionado al costo de transporte desde la planta a cada almacen.

*Cuando no se cubren todas las cantidades de Demanda u Oferta, se agrega una columna ficticia

Método de Transporte

Es una forma del Método Simplex y de Programacion Lineal para resolver situaciones de Origen - Destino.

a) Oferta = Demanda
b) Debe haber linealidad
c) n= filas m= columnas n+m-1

*Basandose en el Método de la Esquina Noroeste

Método de las 2 Fases

La desventaja de la técnica de la "M" es el posible error de cómputo que podría resultar de asignar un valor muy grnade a la constante M. Esta situacion podría presentar errores de redondeo en las operaciones de la computadora digital. Para evitar esta dificultad el problema se puede resolver en 2 fases.

Fase 1. Formula un nuevo problema reemplazando la funcion objetivo por la suma de variables artificiales
La nueva funcion objetivo se minimiza sujeta a las restricciones del problema original. Si el problema tiene un espacion factible el valor mínimo de la F.O. óptima cera cero, lo cual indica que todas las variables artificiales son cero. En este momento pasa a la fase 2.

*Si el valor mínimo de la F.O. óptima es mayor que cero el problema no tiene solución y termina anotándose que no existen soluciones factibles.

Fase 2. Utilice la solución óptima de la fase 1 como solución de inicio para el problema original. En este caso la F.O original se expresa en términos de las variables no básicas utilizando las eliminaciones usuales , Gauss- Jordan.

Ejercicio del Método de la gran "M"

Pasos:


1. Pasar a la forma Estandar el Modelo Matemático
2. Agregar variable artificial donde no hay variable de holgura
3.Penalizar las variables artificiales en la funcion objetivo asignando coeficiente positivo muy grande "M" (minimizar = +M, maximizar= -M)
4.Quitar las "m" de la columna artificial, ya teniendo solucion inicial
5.Se aplica el Método Simplex


Maximizar z= 3x1 + 5x2

x1 ≤ 4
2x2 ≤ 12
3x1+2x2=18

x1, x2 ≥ 0


*La funcion objetivo se debe penalizar con -M, por ser maximizacion y para hacer z=0 por lo tanto:

z= 3x1 + 5x2 -M, entonces: z-3x1-5x2+M= 0

x1 + H1 = 4
2x2 +H2 = 12
3x1 + 2x2 + A1 = 18





(-MR4+R1)















-3R2+R4; (3M+3)R2+R1









R4(-2)+R3 ; R4 (2M+5)+R1









R3(-1)+R2 ; R3 (9/2)+R1 ; R3(3/2)+R4




Solucion:
x= 2
x2=6
H1=2


x1 + H1 = 4
2x2 + H2 = 12
3x1+2x2 +A1 = 18


Entonces:
2+2 = 4
2(6) + 0 = 12
3(2) + 2(6) +0 =18

Método de la Gran "M"

Consiste en modificar el problema original para dar lugar a un nuevo problema agregando una variable "w" llamada artificial y que se penalizara mediante un costo "M" de valores grandes y positivas de forma arbitraria y esto permite que la funcion objetivo tome valores muy grandes tambien cuando sea minimizacion.
Llgara el momento en uqe "w" salga de la base, en este momento W= 0 y esto indica hber regresado al problema original, pero si se llega a w›0, entonces el problema no tiene solucion.

Min z= Cx + Mw

Sujeta a restricciones y penalizando a Zw1 - Cw1

Condicion de introduccion de las variables
≥ Resta
≤ Suma

Minimización

Cuando en los sistemas de inecuaciones de programacion lineal se presentan una solucion que no es factible debido a que no cumple con la condicion de la No negatividad (x,y ≥ 0) se dice que el sistema de inecuaciones no tiene solucion (absurdo matematico), para el caso de minimizacion y para el método Simplez o tabular.

Para el caso de Minimizacion (Simplex o Tabular)
Los sistemas de inecuaciones que no tengan solucion se deben resolver por los metodos siguientes:
El Metodo de la Gran M
Metodo de las Dos Fases